Шум чтения или 1 электрон как абсолютная единица измерения параметров видеорегистрирующих устройств
А. В. Иванова, М. С. Семин
Одним из основных параметров регистрирующих устройств является
собственный шум, который определяет потенциальную чувствительность
устройства, возможности и особенности его применения. Применительно к видеорегистрирующим устройствам, имеющим цифровой выход, под собственным шумом понимается сквозной шум всех устройств и процессов от захвата фотонов на фоточувствительной поверхности регистратора до преобразования полученного сигнала в цифровую форму.
Мерой шума могут быть различные единицы, однако, с нашей точки зрения, наиболее универсальной единицей (т.е. не требующей дополнительных описаний) является величина сигнала на выходе регистратора, производимого одним электроном
Кроме универсальности, поскольку в количестве электронов может быть выражен и уровень насыщения регистратора (глубина потенциальной ямы) и количество зарегистрированной световой энергии и качество получаемого изображения [1], [2], такая единица оказалась весьма естественной и удобной в расчетах видеоустройств, особенно применительно к регистрации слабых изображений. Причем в последнем случае использование такой единицы гарантирует от иллюзии возможности достижения сверхвысоких чувствительностей [3] и развенчивает недобросовестную рекламу «суперсверхчувствительных» камер [4], [5], [6].
Мерой шума могут быть различные единицы, однако, с нашей точки зрения, наиболее универсальной единицей (т.е. не требующей дополнительных описаний) является величина сигнала на выходе регистратора, производимого одним электроном
Кроме универсальности, поскольку в количестве электронов может быть выражен и уровень насыщения регистратора (глубина потенциальной ямы) и количество зарегистрированной световой энергии и качество получаемого изображения [1], [2], такая единица оказалась весьма естественной и удобной в расчетах видеоустройств, особенно применительно к регистрации слабых изображений. Причем в последнем случае использование такой единицы гарантирует от иллюзии возможности достижения сверхвысоких чувствительностей [3] и развенчивает недобросовестную рекламу «суперсверхчувствительных» камер [4], [5], [6].
Определения
Одним из основных параметров регистрирующих устройств является собственный шум, который определяет потенциальную чувствительность устройства, возможности и особенности его применения.Все дальнейшие рассуждения исходят из следующих определений:
- за единицу измерения «1 электрон» - [e] принимается величина сигнала, возникающая на выходе устройства при регистрации одного фотоэлектрона
- под шумом изображения понимается с.к.о. видеосигнала на выходе
- АЦП, обусловленное квантовым шумом, возникающим в процессе накопления зарядовых пакетов в ячейках матрицы, и шумом считывания
- под шумом чтения понимается с.к.о. видеосигнала на выходе АЦП, обусловленное погрешностями, возникающими в процессе переноса зарядовых пакетов в выходной каскад матрицы, шумом выходных каскадов матрицы и шумом аналого-цифрового преобразования;
- под синхронными шумами электроники понимаются повторяющиеся от ввода к вводу шумы, имеющие вид добавленного к основному слабого повторяющегося изображения;
Теоретические положения
Согласно принятым определениям дисперсия количества фотоэлектронов в каждой ячейке матрицы, образующихся при регистрации изображения (Dи), обуславливается квантовым шумом и шумом чтения:| Dи = Dк + Dч | (1) |
где:
Dк – дисперсия квантового шума;
Dч – дисперсия шума чтения,
Дисперсия количества фотоэлектронов в ячейках матрицы вследствие квантового шума (без учета шума чтения) для N последовательных регистраций изображения Dк[e] может быть определена как:
| Dк [e] = 1 / N | (2) |
где:
Si[e] – количество фотоэлектронов в i-той регистрации;
M[e] – среднее значение количества фотоэлектронов в ячейке матрицы в N регистрациях.
При этом для квантового шума справедливо (статистика Пуассона), что дисперсия значений в каждой отдельной ячейке матрицы, выраженная в количестве квантов (в данном случае фотоэлектронов), численно равна математическому ожиданию их количества:
Si[e] – количество фотоэлектронов в i-той регистрации;
M[e] – среднее значение количества фотоэлектронов в ячейке матрицы в N регистрациях.
При этом для квантового шума справедливо (статистика Пуассона), что дисперсия значений в каждой отдельной ячейке матрицы, выраженная в количестве квантов (в данном случае фотоэлектронов), численно равна математическому ожиданию их количества:
| Dк [e] = M[e] | (3) |
| Dк [adc] = 1 / N | (4) |
где:
Dк [adc] – дисперсия квантового шума в единицах аналого-цифрового преобразователя;
k – коэффициент перевода единиц АЦП в единицы электронов.
После преобразования выражение (4) принимает вид:
k – коэффициент перевода единиц АЦП в единицы электронов.
После преобразования выражение (4) принимает вид:
| Dк [adc] = k 1 / N |
Dк [adc] = k2 Dk [e] и M[adc] = kM[e] | (5) (6) |
Поскольку величины дисперсии и математического ожидания, выраженные в количестве фотоэлектронов, численно равны (3), то зависимость дисперсии квантового шума от математического ожидания в единицах АЦП может быть получена путем подстановки M[e] в выражение для Dк [adc]:
| | Dк [adc] = k2 ( 1 / k M[adc]) , или окончательно Dк [adc] = k M[adc] |
(7) |
Таким образом, получив экспериментальным путем зависимость дисперсии квантового шума от математического ожидания в единицах аналого-цифрового преобразователя и определив величину коэффициента наклона прямой, которая и есть величина k, можно пересчитать полученные значения в единицы электронов.
Для достоверного определения интересующих нас параметров необходима достаточно большая выборка значений, получение которой от одного элемента матрицы путем последовательного ввода кадров требует значительного времени.
В тоже время, даже для матриц «низкого разрешения» число элементов матрицы, измеряется сотнями тысяч. При этом качество современных матриц таково, что светочувствительность всех их элементов практически одинакова, что позволяет получить нужную выборку из значений различных элементов матрицы, полученных при вводе одного изображения. Тогда методика измерения шума считывания может быть сведена к следующему:
Для достоверного определения интересующих нас параметров необходима достаточно большая выборка значений, получение которой от одного элемента матрицы путем последовательного ввода кадров требует значительного времени.
В тоже время, даже для матриц «низкого разрешения» число элементов матрицы, измеряется сотнями тысяч. При этом качество современных матриц таково, что светочувствительность всех их элементов практически одинакова, что позволяет получить нужную выборку из значений различных элементов матрицы, полученных при вводе одного изображения. Тогда методика измерения шума считывания может быть сведена к следующему:
- вводится серия пар изображений при различных уровнях освещенности в линейной области матрицы в единицах АЦП. Для этого:
- оценивается граница уровня освещенности линейной области матрицы;
- вводятся пары изображений одинаковой освещенности: при нулевой освещенности, при малых и средних освещенностях (для оценки линейности в области малых освещенностей) и освещенностях, соответствующих верхней части линейной области матрицы;
- для каждого уровня освещенности вычисляется математическое ожидание видеосигнала, как среднее значение величин сигналов элементов изображения, и дисперсия видеосигнала, путем вычисления среднего значения квадратов разностей величин сигналов одноименных элементов в парах изображений. При этом искомая дисперсия будет равна половине полученной величины, поскольку при ее вычислении мы использовали разность двух независимых величин, что ведет к удвоению дисперсии результата;
- полученные значения апроксимируются функцией: Dк [adc]= a[adc] +k M[adc];
- полученные величины и зависимости переводятся в количество электронов в соответствии с соотношениями:
M[e] = 1 / k M[adc] , D[e] = 1/k2 D[adc] , a[e] = 1 / k2 a[adc] - определяется с.к.о. шума чтения как корень квадратный величины a[е].
Источники ошибок и методы их парирования
Следует, однако, отметить, что при определении величины шума чтения с помощью указанной методики возможно появление погрешностей, вызванных:
Ошибки, вызванные смещением нуля, могут быть учтены практически полностью путем вычитания из значений математических ожиданий средней величины, полученной при отсутствии освещения.
Обеспечение равномерности освещения всей поверхности матрицы является нетривиальной задачей, требующей определенных усилий при разработке осветителя. Однако, для задачи измерения шума чтения неравномерность освещения, до тех пор пока освещенность различных участков матрицы не выходит за пределы линейной зоны, не влияет на точность измерения, поскольку каждая величина отношения приращения квадратов разностей яркостей одних элементов матрицы из последовательно полученных пар изображений к приращению полусуммы этих разностей является оценкой величины наклона прямой функции D[adc]= a[adc] +k M[adc], которая при усреднении стремится к ней вне зависимости от самой величины яркости:
- смещением уровня нуля АЦП, специально вводимым при настройке для предотвращения появления отрицательных значений напряжений на входе АЦП и приводящим к завышению величины математического ожидания (по п. 2 методики);
- неравномерностью освещения поверхности матрицы по полю, обусловленной качеством осветителя;
- синхронными шумами электроники управления матрицей и электроники преобразований видеосигнала в цифровую форму, которые могут привести к наличию в получаемых изображениях стабильного повторяющегося от ввода к вводу рельефа;
- нестабильностью уровня освещения, которое может привести к тому, что величины разностей получаемых пар изображений по п.2 методики будут иметь постоянную составляющую, увеличивающую величину вычисляемой дисперсии;
- темновыми (тепловыми) шумами, вызванными темновыми фототоками в ячейках матрицы, которые образуют темновой (тепловой) рельеф, увеличивающийся с повышением температуры матрицы и увеличением времени экспозиции.
Ошибки, вызванные смещением нуля, могут быть учтены практически полностью путем вычитания из значений математических ожиданий средней величины, полученной при отсутствии освещения.
Обеспечение равномерности освещения всей поверхности матрицы является нетривиальной задачей, требующей определенных усилий при разработке осветителя. Однако, для задачи измерения шума чтения неравномерность освещения, до тех пор пока освещенность различных участков матрицы не выходит за пределы линейной зоны, не влияет на точность измерения, поскольку каждая величина отношения приращения квадратов разностей яркостей одних элементов матрицы из последовательно полученных пар изображений к приращению полусуммы этих разностей является оценкой величины наклона прямой функции D[adc]= a[adc] +k M[adc], которая при усреднении стремится к ней вне зависимости от самой величины яркости:
| 1 | 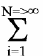 | 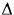 (Sji-Sgi)2 (Sji-Sgi)2 | |
 |  | => k , | |
| 2 N | 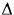 (Sji-Sgi)/2 (Sji-Sgi)/2 |
где:
Sji сигнал i-го элемента первого изображения пары,
Sgi сигнал i-го элемента второго изображения пары.
Следовательно, при условии вычисления среднего значения квадратов разностей и математического ожидания яркостей по одной и той же группе элементов мы всегда будем получать одно из значений одной и той же функции. Из этого следует и то, что, в случае неравномерного освещения поверхности матрицы, можно получать выборки значений сигналов, по произвольно выбранным элементам, приходящимся на участки с разными уровнями освещения, получая при этом корректное значение искомой функции.
Ошибки, вызванные синхронными шумами электроники, исключаются самой методикой измерений, поскольку эти и так малые шумы вычитаются в процессе вычислений как повторяющиеся (см. раздел «Определения»).
Погрешность, связанная с изменением уровня освещения в процессе получения пары изображений может внести существенную ошибку в вычисляемые разности. Для парирования этой погрешности следует вычислить математические ожидания яркостей первого Mj[adc] и второго Mg[adc] изображения пары, затем умножить значения яркостей элементов второго изображения на коэффициент:
Sji сигнал i-го элемента первого изображения пары,
Sgi сигнал i-го элемента второго изображения пары.
Следовательно, при условии вычисления среднего значения квадратов разностей и математического ожидания яркостей по одной и той же группе элементов мы всегда будем получать одно из значений одной и той же функции. Из этого следует и то, что, в случае неравномерного освещения поверхности матрицы, можно получать выборки значений сигналов, по произвольно выбранным элементам, приходящимся на участки с разными уровнями освещения, получая при этом корректное значение искомой функции.
Ошибки, вызванные синхронными шумами электроники, исключаются самой методикой измерений, поскольку эти и так малые шумы вычитаются в процессе вычислений как повторяющиеся (см. раздел «Определения»).
Погрешность, связанная с изменением уровня освещения в процессе получения пары изображений может внести существенную ошибку в вычисляемые разности. Для парирования этой погрешности следует вычислить математические ожидания яркостей первого Mj[adc] и второго Mg[adc] изображения пары, затем умножить значения яркостей элементов второго изображения на коэффициент:
| Mj[adc] | ||
 | ||
| Mg[adc] |
и после этого провести вычисления по предложенной методике.
Ошибки, связанные с тепловыми шумами, хотя и имеют другую природу чем синхронные шумы электроники, также имеют малые значения и также исключаются при вычислениях по предложенной методике.
Ошибки, связанные с тепловыми шумами, хотя и имеют другую природу чем синхронные шумы электроники, также имеют малые значения и также исключаются при вычислениях по предложенной методике.
Методика измерения шума чтения камеры
Исходя из сказанного выше предлагается следующая уточненная методика измерения шума чтения камеры:- оценивается граница уровня освещенности линейной области матрицы;
- вводятся серии пар изображений при:
- нулевой освещенности;
- малых и средних освещенностях;
- освещенностях, соответствующих верхней части линейной области матрицы;
- вычисляется математическое ожидание сигналов при нулевой освещенности M0[adc];
- все полученные значения сигналов уменьшаются на величину M0[adc];
- для каждой пары изображений вычисляются математические ожидания величин сигналов элементов изображения для первого Mj[adc] и второго Mg[adc] ввода изображений:
- величины сигналов второго изображения из полученной пары корректируются путем умножения на величину:
Mj[adc] 
Mg[adc] - вычисляется дисперсия сигнала как среднее значения квадратов разностей
величин сигналов соответствующих элементов в парах изображений,
деленное на два:
1 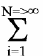
D[adc] = 
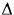 (Sji-Sgi)2
(Sji-Sgi)22 N - полученные значения апроксимируются функцией: D[adc]= a[adc] + kMj[adc], из которой определяется значение коэффициента k;
- полученные величины и зависимости переводятся в количество электронов в соответствии с соотношениями
M[e] = 1/k M[adc] ,
D[e] = 1/k2 D[adc] ,
a[e] = 1/k2 a[adc] - определяется с.к.о. шума чтения как корень квадратный величины a[е].
Список литературы:
- Майоров В.П., Семин М.С. Фотоны и электроны - когда их мало и много, или «шумел фотон 2». «Красный угол» N13 15.06.06.
- Майоров В.П. Почему человек видит то, что не видит компьютер? «Красный угол» N13 15.06.06.
- Крутик М. И. Майоров В.П. Люмены, канделы, ватты и фотоны. Различные единицы - различные результаты измерения чувствительности телевизионных камер на основе ЭОП и ПЗС. "Специальная техника", №5, 2002г., и «Красный угол» N8 26.09.02.
- "А ведь мы уже давно говорим об этом!". «Красный угол» N10 10.09.03.
- Семин М. С. Мы не творим чудес, мы делаем то, что позволяет природа. «Красный угол» N9 22.04.03.
- Семин М.С. Как ответить на вопрос: "А какая у ваших ПЗС камер чувствительность?". «Красный угол» N5 26.10.00.
