Метод гармонической сегментации тоновых цифровых изображений и его применение при геологическом дешифрировании космо- и аэрофотоснимков
"Сегментация изображения представляет собой разделение или разбиение изображение на области по сходству свойств их точек" [1]. Первичное выделение на исходном тоновом изображении возможных искомых объектов при помощи преобразования сегментации является одним из основных этапов анализа изображений. В настоящее время считаются основными два наиболее широко используемых преобразования: яркостное и контурное [2]. Некоторые исследователи включают в состав основных методов также и текстурную сегментацию [3]. Согласно этой классификации, выделение областей в процессе сегментации осуществляется исходя из оценки соответствия, некоторому критерию однородности (сходства) значений: либо яркости I(x,y) каждой точки, либо первой производной 2I(x,y)/ x y яркости в некоторой заданной окрестности каждой точки, либо той или иной текстурной характеристики распределения яркости H(x,y) в заданной окрестности точки [1,3].
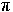 ),
то значение свертки Y N для каждого элемента цифрового изображения,
представляющее собой интеграл Дюамеля [5], в общем случае определяется
выражением:
),
то значение свертки Y N для каждого элемента цифрового изображения,
представляющее собой интеграл Дюамеля [5], в общем случае определяется
выражением:
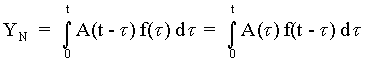 ,
,
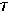 )
в точке (x,y) есть разность спектров исходной свертки и аппаратной функции
дискретизации этого сигнала. Кроме того, саму свертку в каждой точке цифрового
изображения можно рассматривать, как прямоугольный импульсный сигнал с
непрерывным Фурье-спектром. Так же, при анализе прямоугольного импульса,
который может быть определен, как единичный, можно постулировать, что при
процессе сегментации в дискретном пространстве только первый элемент Фурье-образа
такого импульса может рассматриваться, как принадлежащий образу сигнала,
а все остальные - образам аппаратной функции, и могут быть исключены из
процесса анализа. Поскольку цифровое изображение представляет собой область
дискретного пространства, следовательно, при анализе соответствующих Фурье-образов
можно ограничиться рассмотрением только тех элементов спектра, которые
соответствуют существующим в этом пространстве дискретным значениям и не
рассматривать гармоники с периодом, меньшим величины шага дискретизации
(квантования) исходного изображения. Можно показать, что при соблюдении
вышеперечисленных условий, спектр свертки может рассматриваться, как дискретный
и обладающий конечным набором гармоник.
)
в точке (x,y) есть разность спектров исходной свертки и аппаратной функции
дискретизации этого сигнала. Кроме того, саму свертку в каждой точке цифрового
изображения можно рассматривать, как прямоугольный импульсный сигнал с
непрерывным Фурье-спектром. Так же, при анализе прямоугольного импульса,
который может быть определен, как единичный, можно постулировать, что при
процессе сегментации в дискретном пространстве только первый элемент Фурье-образа
такого импульса может рассматриваться, как принадлежащий образу сигнала,
а все остальные - образам аппаратной функции, и могут быть исключены из
процесса анализа. Поскольку цифровое изображение представляет собой область
дискретного пространства, следовательно, при анализе соответствующих Фурье-образов
можно ограничиться рассмотрением только тех элементов спектра, которые
соответствуют существующим в этом пространстве дискретным значениям и не
рассматривать гармоники с периодом, меньшим величины шага дискретизации
(квантования) исходного изображения. Можно показать, что при соблюдении
вышеперечисленных условий, спектр свертки может рассматриваться, как дискретный
и обладающий конечным набором гармоник.
( 2 ) 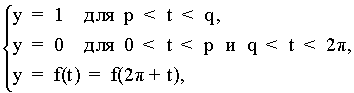
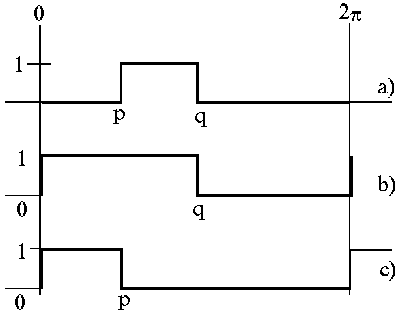
и представлена графиком, приведенном на Рис. 1-a, либо, если p или q равны нулю, графиками, приведенными на Рис. 1-b,-c.
Обозначив функцию ( 2 ) символом 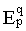 и
поскольку это периодическая функция с периодом, равным 2
и
поскольку это периодическая функция с периодом, равным 2 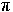 , то по определению имеем:
, то по определению имеем:
( 3 ) ![]()
![]() .
.
При этом справедливо равенство
( 4 ) ![]()
![]() ,
,
смысл которого иллюстрируется Рис. 1-b и Рис. 1-c.
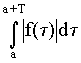 ,
существует и бесконечный тригонометрический ряд:
,
существует и бесконечный тригонометрический ряд:
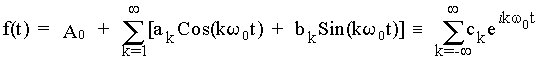
где
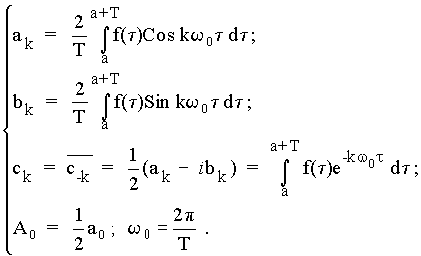
При преобразовании функций ( 3 ) и ( 4 ) обозначим эти
коэффициенты, соответственно, символами ![]() .
Кроме того, подставляя выражения ( 6 ) в ( 5 ) и полагая Т = 2
.
Кроме того, подставляя выражения ( 6 ) в ( 5 ) и полагая Т = 2 ![]() и, следовательно, w
и, следовательно, w ![]() = 1, получим:
= 1, получим:
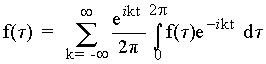 .
.
( 8 ) 
( 9 ) ![]()
где i = 0, a, b, ..., n; j = a, b, ..., 2 ![]() . И следовательно, если
. И следовательно, если ![]() -
коэффициенты F(x), аналогичные коэффициентам ряда Фурье, то
-
коэффициенты F(x), аналогичные коэффициентам ряда Фурье, то
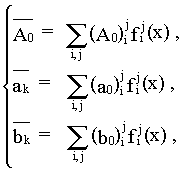
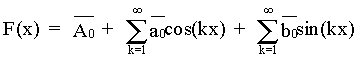
является рядом Фурье.
( 12 ) 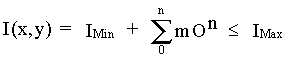
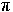 , где
, где
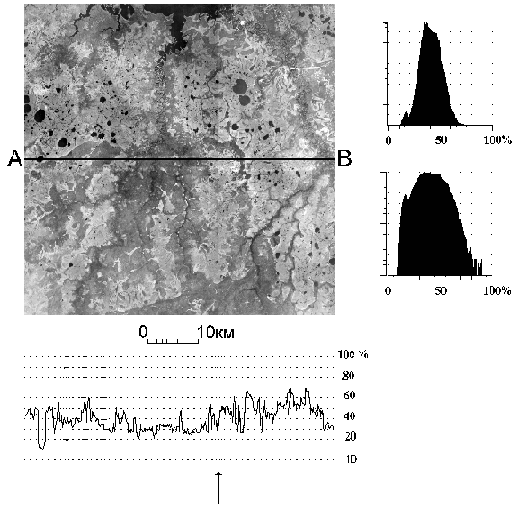
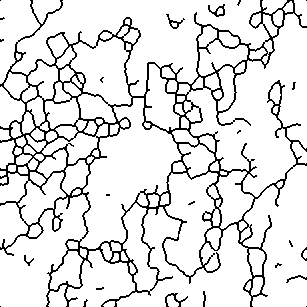
Рис. 2. Исходное изображение.
|
|
|
| Размер видеоматрицы (пикс.) |
|
| Линейный масштаб (км/пикс.) |
|
| Размер изображения (км) |
|
| Площадь изображения (пикс. 2 ) |
|
| Площадь изображения (км 2 ) |
|
| Минимальная яркость |
|
| Максимальная яркость |
|
| Средняя яркость (%) |
|
| Мода яркости |
|
| Абсолютное s (%) |
|
| Относительное s (относит. %) |
|
| Девиация (%) |
|
| Асимметрия |
|
| Эксцесс |
|
| Энергия |
|
| Энтропия |
|
Достаточно легко показать, что выделение необходимой информации при помощи распространенных методов сегментации чрезвычайно неэффективно и требует большего объема ручных методов интерпретации. Таким образом, высокий уровень шумов изображения ограничивает выбор методов сегментации для выделения объектов, связанных с тектоническими структурами района, и делает наиболее предпочтительным в качестве базового метода выбор гармонической сегментации, как наиболее помехоустойчивого. Кроме того, высокий уровень помех, определяемых качеством исходного изображения, при попытке получить более четкие и надежные результаты анализа требует проведения комплексной текстурно-гармонической сегментации, основанной на оценке однородности не только по заданному набору гармонических составляющих, но и по их соответствующим текстурным признакам.
Преобразование комплексной гармонической сегментации в данном случае
заключалась в следующей последовательности операций. На первом этапе яркостные
значения исходного изображения оптимизировались преобразованием расширения
яркостного диапазона [1,3] до 100%. Затем, принимая стандартный интервал
разложения яркостного сигнала Т = 2 ![]() и нормируя на него величину диапазона всех возможных значений результатов
свертки сигнала в пределах окна (2N+1)(2M+1) элементов, формировался набор
признаков
и нормируя на него величину диапазона всех возможных значений результатов
свертки сигнала в пределах окна (2N+1)(2M+1) элементов, формировался набор
признаков ![]() B(n,m)
= f(
B(n,m)
= f( ![]() ) для
гармонической сегментации, в соответствии с выражением ( 7 ). В данном
случае, в качестве исходного сигнала использовалась свертка значений яркости
исходного изображения, в пределах прямоугольного окна размером 0.2379 *
0.2379 км (0.0566 км 2 ). В качестве признаков сегментации использовался
стандартный набор последовательных гармонических составляющих с относительными
частотами
) для
гармонической сегментации, в соответствии с выражением ( 7 ). В данном
случае, в качестве исходного сигнала использовалась свертка значений яркости
исходного изображения, в пределах прямоугольного окна размером 0.2379 *
0.2379 км (0.0566 км 2 ). В качестве признаков сегментации использовался
стандартный набор последовательных гармонических составляющих с относительными
частотами ![]() n
равными
1/
n
равными
1/ ![]() , 2/
, 2/ ![]() , 4/
, 4/ ![]() ,
... , то есть, соответственно, 1-я, 2-я, 3-я, ... взаимно-кратные гармоники
(далее, просто гармоники) Фурье-образа свертки. Верхний и нижний значения
критерии однородности (пороги обнаружения) задавались таким образом, чтобы
интервал однородности вмещал лишь одну взаимно-кратную гармонику. Для каждого
значения исходного сигнала заданной окрестности каждой точки изображения
автоматически выделялось и анализировалось 12 гармоник.
,
... , то есть, соответственно, 1-я, 2-я, 3-я, ... взаимно-кратные гармоники
(далее, просто гармоники) Фурье-образа свертки. Верхний и нижний значения
критерии однородности (пороги обнаружения) задавались таким образом, чтобы
интервал однородности вмещал лишь одну взаимно-кратную гармонику. Для каждого
значения исходного сигнала заданной окрестности каждой точки изображения
автоматически выделялось и анализировалось 12 гармоник.
Суть текстурно-гармонической сегментации заключалась в том, что выделение областей однородности осуществлялось путем классической текстурной сегментации [1], при которой в качестве базовой функции для формирования модифицированного текстурного признака использовались результаты гармонической сегментации яркостного сигнала. Модифицированный текстурный признак T(j,k), в данной работе - признак Розенфельда и Троя [7], формировался на прямоугольном окне(2N+1)(2M+1) элементов в соответствии с выражением:
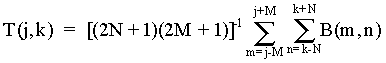 ,
,

а) |

б) |
а) Результаты гармонической сегментации с прямоугольным окном свертки, размером 0.2379 ? 0.2379 км (0.0566 км 2 ).
б) Результаты текстурно-гармонической сегментации. Окно свертки: 0.2379 * 0.2379 км (0.0566 км 2 ). Область текстурной оценки: 0.5551 * 0.5551 км (0.3081 км 2 ); интервал критерия однородности: 49,0%- 100%.
Результаты анализа данных рассмотренных выше методов сегментации
изображения, приведенного на Рис. 1, можно резюмировать следующим образом.
Первая гармоника с относительной частотой ![]() n
= 1/
n
= 1/ ![]() на
изображении практически отсутствует, что определяется его низким качеством.
С увеличением номера (частоты) иных гармонических составляющих наблюдается
существенное падение отношения сигнал-шум, но лучшие результаты дает текстурно-гармоническая
сегментация.
на
изображении практически отсутствует, что определяется его низким качеством.
С увеличением номера (частоты) иных гармонических составляющих наблюдается
существенное падение отношения сигнал-шум, но лучшие результаты дает текстурно-гармоническая
сегментация.
На Рис. 3 приведены результаты гармонической и текстурно-гармонической
сегментаций исходного изображения, приведенного на Рис. 1. В обоих этих
случаях в качестве базовой функции была выбраны области распространения
гармонической составляющей с относительной частотой ![]() n
= 2/
n
= 2/ ![]() (2-я
гармоника). Сравнение результатов, приведенных на Рис. 3, наглядно показывает,
что для решения поставленной задачи можно воспользоваться, как гармонической,
так и текстурно-гармонической сегментацией, но отношение сигнал-шум в последнем
случае существенно выше. Шумовая составляющая результатов гармонической
сегментации, выражающаяся в большом количестве мелкоплощадных (точечных)
сигналов, высокой изрезанности границ и т.п., на изображении Рис. 3-а достаточно
велика. Однако, также хорошо видно, что и в этом случае влияние помех,
вызванных дефектами изображения, уже сведено к минимуму, хотя, например,
следы вертикальной границы общего перепада яркости и светлых горизонтальных
полос все еще прослеживаются. На изображении Рис. 3-б высокочастотные пространственные
шумовые составляющие практически отсутствуют, что заставляет считать преобразование
текстурно-гармонической сегментации в данном случае предпочтительным. То
же самое наблюдается для пространственных распределений всех остальных
гармоник.
(2-я
гармоника). Сравнение результатов, приведенных на Рис. 3, наглядно показывает,
что для решения поставленной задачи можно воспользоваться, как гармонической,
так и текстурно-гармонической сегментацией, но отношение сигнал-шум в последнем
случае существенно выше. Шумовая составляющая результатов гармонической
сегментации, выражающаяся в большом количестве мелкоплощадных (точечных)
сигналов, высокой изрезанности границ и т.п., на изображении Рис. 3-а достаточно
велика. Однако, также хорошо видно, что и в этом случае влияние помех,
вызванных дефектами изображения, уже сведено к минимуму, хотя, например,
следы вертикальной границы общего перепада яркости и светлых горизонтальных
полос все еще прослеживаются. На изображении Рис. 3-б высокочастотные пространственные
шумовые составляющие практически отсутствуют, что заставляет считать преобразование
текстурно-гармонической сегментации в данном случае предпочтительным. То
же самое наблюдается для пространственных распределений всех остальных
гармоник.
При гармонической сегментации для более или менее уверенной интерпретации, для выделения информации, необходимой для тектонического картирования, наиболее подходят области распространения только второй, третьей и четвертой гармоник. В то же время, для анализа информации о тектонических структурах района по результатам текстурно-гармонической сегментации, могут быть уверенно использованы карты-схемы выделенных областей распространения гармонических составляющих уже от второй до пятой гармоник, включительно.

а) |
б) |
Автоматическое выделение этих данных осуществлялось методами контурных трансформаций, включающих комплексные алгоритмы осреднения и построения остова, по участкам максимальных градиентов на границах выделенных областей распространения. В результате были получены карты-схемы машинных линеаментов, как элементарных (Е-линеаментов) так и полных, (Рис.4-а и -б, соответственно) [8], представляющих собой центромеры (осевые линии) соответствующих участков этих областей. Характерной особенностью этого типа обработки информации может явиться практически полная потеря возможности интерпретации исходного структурно-литологического рисунка, но при этом выявляется система (или системы) линий, связанные со скрытыми дислокациями, которые могут быть очень неконтрастно проявлены на исходных тоновых изображениях.
Карта-схема машинных Е-линеаментов (Рис. 4-а) позволяет получить и статистически
обработать информацию о расположении, протяженности и направлении простирания
отдельных отрезков границ выделенных зон, связанных с простиранием соответствующих
тектонических структур. Кроме того, она позволяет осуществить трассирование
этих структур, как по простиранию самих Е-линеаментов, так и по линиям
их УобрываФ. 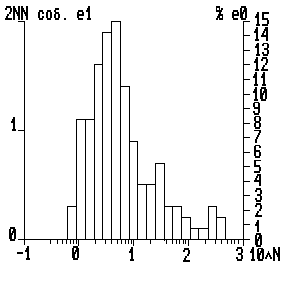
На карте-схеме полных машинных линеаментов (Рис. 4-б), полученные линеаменты образуют планарный граф, разбивающий анализируемый район на отдельные участки, в пределах которых значения яркостных гармонических составляющих могут считаться удовлетворяющими заданному критерию однородности. Выделенные участки можно рассматривать как элементарные объекты, характеризующие тектоническое строение района.
На данном анализируемом изображении присутствует 135 объектов различных форм и размеров, обладающих соответствующими дискриминантными признаками. В качестве одного из возможных направлений дальнейшего количественного анализа, осуществлялся анализ площадей выделенных объектов, распределение которых приведено на Рис. 5.
Анализ распределения величин площадей выделенных участков позволяет достаточно уверенно разбить эти участки на три условных класса, в соответствии с занимаемыми ими площадями. К первому классу можно отнести все участки, площадь которых менее 22 км 2 . Это наиболее многочисленный класс, образующий основной пик статистического распределения. Ко второму классу можно отнести все участки, площадь которых находится в пределах от 22 км 2 до 122 км 2 . Объекты этого класса образуют второй пик гистограммы. К третьему, последнему, классу можно отнести участки с площадью более 122 км 2 . Их количество не может считаться статистически представительным, но разброс их значений выходит далеко за пределы дисперсии, допустимой для объектов второго класса, что в свою очередь, позволяет с достаточной уверенностью выделять их в отдельный класс.
Анализ форм и областей распространения объектов каждого из выделенных классов позволяет делать предположения об их связи с некоторыми определенными тектоническими зонами и структурами.
Расположение объектов первого класса приведено на Рис. 6. Они располагаются узкими вытянутыми зонами, ориентированными в субмеридиональном и юго-западном - северо-восточном (диагональном) направлениях и это обстоятельство подталкивает к выводу о связи этих объектов с активными участками разломных структур. Необходимо отметить, что на изучаемой территории распространен мощный осадочный чехол, мощностью до 3-3,5 км, структура которого хорошо изучена геофизическими методами в интересах нефтедобычи. Результаты этих комплексных исследований указывают на присутствие разломов того же простирания и расположения. Характерной деталью является то, что в пределах выделяемых областей распространения объектов этого класса, было выявлены четкие следы тектонической активности не только при картировании поверхности фундамента, но и в самом осадочном чехле. Также нельзя не отметить, что методы гармонической сегментации автоматического анализа космоизображений более надежно, а главное, с существенно большей производительностью распознают те же разломы в кристаллическом фундаменте.

Расположение объектов второго класса приведено на Рис. 7. Они представляют собой относительно широкие вытянутые области. Положение линий, сопрягающих границы обрисованных площадей, совпадает с хорошо известными долгоживущими разломными структурами фундамента, и их проявление на поверхности является некоторой неожиданностью, так как другими методами выявить их распространение в осадочном чехле, а тем более на поверхности, не удавалось. Они выявляются только при картировании фундамента, соответствующими методами.

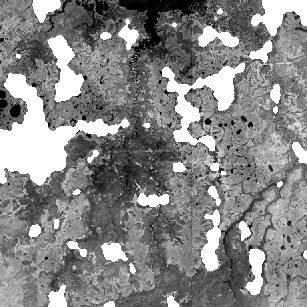
Рис. 8. Области распространения участков с площадями более 122 км 2 . (выделены белым цветом).
Расположение объектов третьего класса приведено на Рис. 8. Они представляют собой обширные области сложной формы, связанными с крупными консолидированными участками коренных пород с низкой тектонической активностью в их пределах. Это предположение подтверждается и имеющимися геолого-геофизическими данными. Таким образом, анализ изображения площади способен дать не менее четкую картину распространения разломных зон, чем геофизические методы.
Метод гармонической сегментации тоновых цифровых изображений используемый для структурно-тектонического дешифрирования космоизображений дает вполне информативные результаты, не противоречащие геофизическим данным и данным, полученным при бурении скважин. В пределах поставленной задачи были даны ответы на вопросы об общем тектоническом строении представленной на анализируемом фотоснимке территории. При сопоставлении этих результатов с результатами традиционного (ручного линеаментного анализа) обнаруживается их достаточно хорошая сходимость. Представляется, что данный метод вполне может широко использоваться в геолого-поисковых работах. В качестве его развития необходимо, конечно иметь в виду необходимость его сопряжения с геоинформационными системами (ГИС) для более строгой привязки результатов анализа к местности
В заключение необходимо указать на достаточно важный прикладной аспект применения метода гармонической сегментации - его высокую производительность. Учитывая, что размер анализируемого изображения может быть произвольным, дать строгую оценку временных затрат на сегментацию одного изображения представляется затруднительным. Поэтому, в качестве примерной оценки, могут быть использованы временные затраты на обработку 1 пиксела изображения любого размера. При проведении настоящих работ использовалась аппаратно-программный комплекс анализа изображений (на базе IBM PC/AT) "Видео-Мастер 60.2", производства НВП "Центр", с системами ввода изображений: VS60, производства фирмы "Видеоскан", ScanNex II, производства АО "Экстел", и со стандартного планшетного сканера. В компьютере использовался процессор Pentium Pro с тактовой частотой 66 МГц. Размеры анализируемого цифрового изображения составляли 768? 768 пикселов. При размещении результатов в ОЗУ компьютера, временные затраты на процесс преобразования гармонической сегментации составляли около 1 микросекунды на пиксел. Размещение результатов в виртуальной дисковой памяти увеличивало затраты времени примерно на 2-2,5 порядка и они составляли около 100 микросекунд на пиксел, что тоже может считаться достаточно высокой производительностью. В данном конкретном случае, общие временные затраты на анализ всего космоизображения, с учетом затрат, вызванных весьма несовершенной технологии ввода-вывода данных и подготовкой отчета, составили менее недели, в то время как на линеаментные анализы соответствующих фото- и картографических источников тратятся недели и месяцы работы высококвалифицированных специалистов.
Литература.
- Прэтт У.К. Цифровая обработка изображений./ Пер. с англ. - М.: Мир, 1982, кн. 1, 2, 790 с. (William K. Pratt. Digital Image Processing. - A Willey - Interscience Publication. John Willey and Sons. 1978.)
- Яншин В.В. Анализ и обработка изображений: принципы и алгоритмы. - М.: Машиностроение. 1995. - 112 с.: ил.
- Павлидис Т. Алгоритмы машинной графики и обработки изображений./ Пер. с англ. - М.: Радио и связь, 1986, 400 с. (Pavlidis T. Algorithms for Graphics and Image Processing. - Computer Science Press, Inc., 1982.)
- Бейтс Р, Мак-Доннел М. Восстановление и реконструкция изображений. / Пер. с англ. - М.: Мир, 1989. - 336 с. (Bates R.H.T., McDonnell M.J. Image Restoration and Reconstruction. - Clarendon Press-Oxford, 1986.)
- Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. - М.: Наука, 1974, 831 с. (Korn Granino A., Korn Theresa M. Mathematical Handbook for Scientists and Engineers. - New York, San Francisco, Toronto, London, Sydney: Mc-Graw-Hill Book Company, 1968.).
- Мэнли Р. Анализ и обработка записей колебаний. / Пер. С англ. - М.: УМашиностроениеФ, 1972, 368 с. (Manley R.G. Waveform Analysis (A guide to the interpretation of periodic waves, incluing vibration records). - New York, John Wiley and Sons Inc., 1948)/
- Rosenfeld A.A., Troy E.B. Visual Texture Analysis./ In Proc. UMR-Mervin J. Kelly Communication Conf. - Missuri: University of Misscuri-Rolla, Oct. 1970, Section 10-1.
- Данильченко А.Я., Марков М.С., Островский М.В., Тюфлин Ю.С. Автоматизированное выделение и анализ линеаментов по радиолокационным изображениям Венеры. - Геодезия и картография, 1989, ч 7, c. 23-26.
